如图所示，质量为m的物体，放在一固定斜面上，当斜面倾角为300时恰能沿斜面匀速下滑。保持斜面倾角为300，对物体施加一水平向右的恒力F，使物体沿斜面匀速向上滑行，已知重力加速度为g，试求：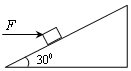
（1）物体与斜面间的动摩擦因数μ；
（2）水平恒力F的大小；
如图所示，小物块A、B由跨过定滑轮的轻绳相连，A置于倾角为37°的光滑固定斜面上，B位于水平传送带的左端，轻绳分别与斜面、传送带平行。传送带始终以速度v0=2m/s向右匀速运动，某时刻B从传送带左端以速度v1=6m/s向右运动，经一段时间回到传送带的左端。已知A、B质量均为1kg，B与传送带间的动摩擦因数为0.2，斜面、轻绳、传送带均足够长，A不会碰到定滑轮，定滑轮的质量与摩擦均不计。g取 10m/s2，sin37°=0.6。求：
⑴B向右运动的总时间；
⑵B回到传送带左端时的速度；
⑶上述过程中B与传送带间因摩擦产生的总热量。
(12分) 如图，等量异种点电荷，固定在水平线上的M、N两点上，有一质量为m、电荷量为＋q（可视为点电荷）的小球，固定在长为L的绝缘轻质细杆的一端，细杆另一端可绕过O点且与MN垂直的水平轴无摩擦地转动，O点位于MN的垂直平分线上距MN为L处。现在把杆拉起到水平位置，由静止释放，小球经过最低点B时速度为v，取O点电势为零，忽略q对等量异种电荷形成电场的影响。求：
(1)小球经过B点时对杆的拉力大小；
(2)在＋Q、－Q形成的电场中，A点的电势φA；
(3)小球继续向左摆动，经过与A等高度的C点时的速度大小。
(9分)一个人最多能提起质量m0=20kg的重物。在倾角θ=15°的固定斜面上放置一物体（可视为质点），物体与斜面间动摩擦因数
。设最大静摩擦力等于滑动摩擦力，求人能够向上拖动该重物质量的最大值m。
如图甲所示，固定在水平桌边上的“ ”型平行金属导轨足够长，倾角为53º，间距L=2m，电阻不计；导轨上两根金属棒ab、cd的阻值分别为R1=2Ω，R2=4Ω，cd棒质量m1=1.0kg，ab与导轨间摩擦不计，cd与导轨间的动摩擦因数μ=0.5，设最大静摩擦力等于滑动摩擦力，整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中。现让ab棒从导轨上某处由静止释放，当它刚要滑出导轨时，cd棒刚要开始滑动；g取10m／s2，sin37 º ="cos53" º =0.6，cos37 º =" sin53" º =0.8。
(1)在乙图中画出此时cd棒的受力示意图，并求出ab棒的速度；
(2)若ab棒无论从多高的位置释放，cd棒都不动，则ab棒质量应小于多少？
(3)假如cd棒与导轨间的动摩擦因数可以改变，则当动摩擦因数满足什么条件时，无论ab棒质量多大、从多高位置释放，cd棒始终不动？
粤公网安备 44130202000953号