如图所示,在匀强电场中建立直角坐标系xoy,y轴竖直向上,一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线
运动,重力加速度为g。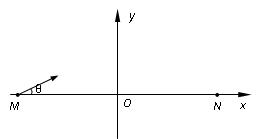
(1)求匀强电场场强E的大小及方向;
(2)若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点,M、N两点关于原点o对称,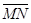 =L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
=L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
如图所示,在匀强电场中建立直角坐标系xoy,y轴竖直向上,一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线
运动,重力加速度为g。
(1)求匀强电场场强E的大小及方向;
(2)若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点,M、N两点关于原点o对称,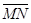 =L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
=L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。