如下图所示，长为L平台固定在地面上，平台的上平面光滑，平台上放有小物体 A和B，两者彼此接触。物体A的上表面是半径为R（R<<L）的光滑半圆形轨道，轨道顶端有一小物体C，A、B、C的质量均为m。现物体C从静止状态沿轨道下滑，已知在运动 过程中，A、C始终保持接触。试求：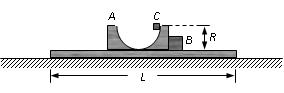
（1）物体A和B刚分离时，物体B的速度。
（2）物体A和B刚分离后，物体C所能达到距台面的最大高度。
（3）判断物体A从平台左边还是右边落地并简要说明理由。
如图是一个十字路口的示意图，每条停车线到十字路中心O的距离均为20m。一人骑电动助力车以7m/s的速度到达停车线（图中A点）时，发现左前方道路一辆轿车正以8m/s的速度驶来，车头已抵达停车线（图中B），设两车均沿道路中央作直线运动，助力车可视为质点，轿车长4.8m，宽度可不计。
（1）请通过计算判断两车保持上述速度匀速运动，是否会发生相撞事故？
（2）若轿车保持上述速度匀速运动，而助力车立即作匀加速直线运动，为避免发生相撞事故，助力车的加速度至少要多大？
如图所示，跳伞运动员做低空跳伞表演，他在离地面224m高处，由静止开始在竖直方向做自由落体运动．一段时间后，立即打开降落伞，并以12.5m/s2的加速度匀减速下降，为了运动员的安全，要求运动员落地速度最大不得超过5m/s(g取10m/s2)．求运动员展开伞时，离地面高度至少为多少？着地时相当于从多高处自由落下？
一辆卡车以v=12m/s的速度匀速行驶，因路口红灯，开始以a=2m/s2的加速度刹车，求：
（1）卡车在3s末的速度v
（2）卡车在第6s内的位移x1
（3）卡车在8s内的位移x2与平均速度
从车站开出的汽车，做匀加速直线运动，开出12 s后，发现还有乘客没上来，于是立即做匀减速运动直至停车。汽车从开出到停止总共历时20 s，行进了50 m．求汽车在此过程中的最大速度．
粤公网安备 44130202000953号