一个质量为m=1.0×10-7kg，带电量为q=1.0×10-10C的微粒，从A点射入一竖直向上匀强电场中，微粒恰好做匀速直线运动,如图所示，虚线为微粒运动轨迹与水平方向成45°角。（取g=10m/s2,结果保留两位有效数字）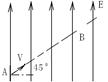
（1）电场强度的大小是多少？
（2）若AB相距14.14cm，则微粒从AB间电势差是多少？
相关试题
土星周围有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动.其中有两个岩石颗粒A和B与土星中心的距离分别为rA=8.0×104 km和rB=1.2×105 km,忽略所有岩石颗粒间的相互作用.(结果可用根式表示),求:
(1)岩石颗粒A和B的线速度之比.
(2)岩石颗粒A和B的周期之比.
(3)土星探测器上有一物体,在地球上重为10 N,推算出它在距土星中心3.2×105 km处受到土星的引力为0.38 N.已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?
宇航员站在一质量分布均匀星球表面上某高h处，沿水平方向抛出一个小球．测得落地时间为t．该星球的半径为R，万有引力常量为G，求
(1)该星球的质量M．
(2)该星球的密度
(3)该星球的第一宇宙速度
，地球表面的重力加速度为g，在赤道上空一颗相对地球静止的同步卫星离地面的高度h是多少?（用以上三个量表示）
粤公网安备 44130202000953号