有人设计了一种可测速的跑步机,测速原理如图所示,该机底面固定有间距为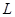 、长度为
、长度为 的平行金属电极。电极间充满磁感应强度为
的平行金属电极。电极间充满磁感应强度为 、方向垂直纸面向里的匀强磁场,且接有电压表和电阻
、方向垂直纸面向里的匀强磁场,且接有电压表和电阻 ,绝缘橡胶带上镀有间距为
,绝缘橡胶带上镀有间距为 的平行细金属条,磁场中始终仅有一根金属条,且与电极接触良好,不计金属电阻,若橡胶带匀速运动时,电压表读数为
的平行细金属条,磁场中始终仅有一根金属条,且与电极接触良好,不计金属电阻,若橡胶带匀速运动时,电压表读数为 ,求:
,求: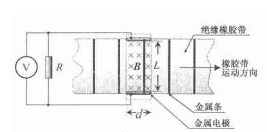
(1)橡胶带匀速运动的速率;
(2)一根金属条每次经过磁场区域克服安培力做的功。
相关知识点
有人设计了一种可测速的跑步机,测速原理如图所示,该机底面固定有间距为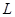 、长度为
、长度为 的平行金属电极。电极间充满磁感应强度为
的平行金属电极。电极间充满磁感应强度为 、方向垂直纸面向里的匀强磁场,且接有电压表和电阻
、方向垂直纸面向里的匀强磁场,且接有电压表和电阻 ,绝缘橡胶带上镀有间距为
,绝缘橡胶带上镀有间距为 的平行细金属条,磁场中始终仅有一根金属条,且与电极接触良好,不计金属电阻,若橡胶带匀速运动时,电压表读数为
的平行细金属条,磁场中始终仅有一根金属条,且与电极接触良好,不计金属电阻,若橡胶带匀速运动时,电压表读数为 ,求:
,求:
(1)橡胶带匀速运动的速率;
(2)一根金属条每次经过磁场区域克服安培力做的功。