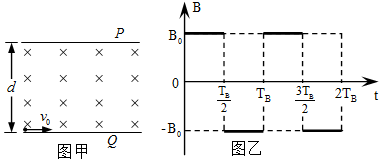
如图甲所示，间距为、垂直于纸面的两平行板、间存在匀强磁场。取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示。时刻，一质量为、带电荷量为的粒子（不计重力），以初速度由板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区。当和取某些特定值时，可使时刻入射的粒子经时间恰能垂直打在板上（不考虑粒子反弹）。上述、、、为已知量。
（1）若，求；
（2）若，求粒子在磁场中运动时加速度的大小；
（3） 若，为使粒子仍能垂直打在板上，求。
如图所示，轻杆两端分别系着质量为
的圆环A和质量为
的小球B，轻杆与A的连接处有光滑铰链，轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上，A、B静止不动时B球恰好与光滑地面接触，在B的左侧是半径为
m的1/4圆弧。质量为
的小球C以
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动，小球B在运动过程中恰好能与横杆接触。重力加速度取
，则:
（1）碰后C球平抛的水平位移（2）碰后瞬间B球的速度（3）A、B间轻杆的长度
如图所示，AB部分是竖直平面内的四分之一圆弧轨道，在下端B与水平直轨道BC相切。一质量为
的小物块，在水平力
的作用下静止于P点。已知PO与水平方向的夹角
，圆弧轨道的半径
，圆弧轨道光滑，物块与水平轨道BC之间的滑动摩擦因数
。重力加速度
.求：
（1）小物块静止于P点时水平力的大小;
（2）撤去水平力，由P点无初速释放小物块，求小物块通过最低点B时轨道对小物块的支持力
;
（3）小物块在水平轨道上滑动的最大距离
.
，地球的自转周期为
，卫星在同步圆轨道上的轨道半径为
，求：地球的半径？在工厂的流水线上安装有传送带，用传送带传送工件，可大大提高工作效率．如题图所示，传送带与水平面夹角为
，其上、下两端点A、B间的距离是3.84m．传送带在电动机的带动下，以4.0m/s顺时针匀速运转．现将质量为10kg的工件（可视为质点）轻放于传送带的A点，已知工件与传送带间的动摩擦因数为
，则在传送带将工件从A点传送到B点过程中，
；求：
（1）物体放上传送带时的加速度大小？
（2）当物体与传送带等速时，传送带立即以8m/s2加速度顺时针匀减速运转，此时物体的摩擦力大小？工件从A点传送到B点的时间？
(3)若传送带因故障被卡住，要使静止工件以（1）问的加速度从A点运动到B点，则需对工件提供的最小拉力为多少？
点，另一端系一质量
的小球，小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放，小球运动到最低点时，轻绳刚好被拉断。
点为顶点的固定斜面，倾角
,斜面足够长，且
，已知重力加速度为
，忽略空气阻力；求：
粤公网安备 44130202000953号