如图，一质量为m=10kg的物体，由1/4圆弧轨道上端从静止开始下滑，到达底端时的速度v=2m/s，然后沿水平面向右滑动1m距离后停止.已知轨道半径R="0." 4m，g=10m/s2，则：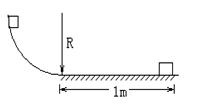
（1）物体滑至圆弧底端时对轨道的压力是多大？
（2）物体与水平面间的动摩擦因数μ是多少？
（3）物体沿圆弧轨道下滑过程中摩擦力做多少功？
在如图所示的竖直平面内，物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接，分别静止于倾角θ＝37°的光滑斜面上的M点和粗糙绝缘水平面上，轻绳与对应平面平行．劲度系数k＝5 N/m的轻弹簧一端固定在O点，一端用另一轻绳穿过固定的光滑小环D与A相连，弹簧处于原长，轻绳恰好拉直，DM垂直于斜面．水平面处于场强E＝5×104 N/C、方向水平向右的匀强电场中．已知A、B的质量分别为mA＝0.1 kg和mB＝0.2 kg，B所带电荷量q＝＋4×10－6 C．设两物体均视为质点，不计滑轮质量和摩擦，绳不可伸长，弹簧始终在弹性限度内，B电荷量不变．取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8.
(1)求B所受静摩擦力的大小；
(2)现对A施加沿斜面向下的拉力F，使A以加速度a＝0.6 m/s2开始做匀加速直线运动．A从M到N的过程中，B的电势能增加了ΔEp＝0.06 J．已知DN沿竖直方向，B与水平面间的动摩擦因数μ＝0.4.求A到达N点时拉力F的瞬时功率．
如图甲所示，足够长的光滑平行金属导轨MN、PQ所在平面与水平面成30°角，两导轨的间距l＝0.50 m，一端接有阻值R＝1.0 Ω的电阻．质量m＝0.10 kg的金属棒ab置于导轨上，与导轨垂直，电阻r＝0.25 Ω.整个装置处于磁感应强度B＝1. 0 T的匀强磁场中，磁场方向垂直于导轨平面向下．t＝0时刻，对金属棒施加一平行于导轨向上的外力F，使之由静止开始运动，运动过程中电路中的电流随时间t变化的关系如图乙所示．电路中其他部分电阻忽略不计，g取10 m/s2.求：
(1)4.0 s末金属棒ab瞬时速度的大小；
(2)3.0 s末力F的瞬时功率；
(3)已知0～4.0 s时间内电阻R上产生的热量为0.64 J，试计算F对金属棒所做的功．
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M板正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．
(1)判断半球面A、B的电势高低，并说明理由；
(2)求等势面C所在处电场强度E的大小；
(3)若半球面A、B和等势面C的电势分别为φA、φB和φC，则到达N板左、右边缘处的电子，经过偏转电场前、后的动能改变量ΔEk左和ΔEk右分别为多少？
(4)比较|ΔEk左|与|ΔEk右|的大小，并说明理由．
如图所示的坐标平面内，y轴左侧存在方向垂直纸面向外、磁感应强度大小B1＝0.20 T的匀强磁场，在y轴的右侧存在方向垂直纸面向里，宽度d＝12.5 cm的匀强磁场B2，某时刻一质量m＝2.0×10－8 kg、电荷量q＝＋4.0×10－4 C的带电微粒(重力可忽略不计)，从x轴上坐标为(－0.25 m,0)的P点以速度v0＝2.0×103 m/s沿y轴正方向运动．试求：
(1)微粒在y轴左侧磁场中运动的轨道半径；
(2)微粒第一次经过y轴时，速度方向与y轴正方向的夹角；
(3)要使微粒不能从右侧磁场边界飞出，B2应满足的条件．
粤公网安备 44130202000953号