如图所示,半径为R的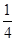 固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高
固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高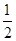 R处由静止释放,重力加速度为g,试求:
R处由静止释放,重力加速度为g,试求:
①在小球A压缩轻质弹簧到弹簧压缩到最短的过程中,弹簧对小球B的冲量大小;
②要使弹簧能再次被压缩,m与M应满足什么关系?
如图所示,半径为R的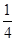 固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高
固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高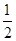 R处由静止释放,重力加速度为g,试求:
R处由静止释放,重力加速度为g,试求:
①在小球A压缩轻质弹簧到弹簧压缩到最短的过程中,弹簧对小球B的冲量大小;
②要使弹簧能再次被压缩,m与M应满足什么关系?