如图所示,压力传感器能测量物体对其正压力的大小,现将质量分别为M、m的物块和小球通过轻绳固定,并跨过两个水平固定的定滑轮(滑轮光滑且较小),当小球在竖直面内左右摆动且高度相等时,物块始终没有离开水平放置的传感器。已知小球摆动偏离竖直方向的最大角度为θ,滑轮O到小球间细线长度为l,重力加速度为g,求:
(1)小球摆到最低点速度大小; (2)小球摆到最低点时,压力传感器示数为0,则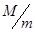 的大小。
的大小。
如图所示,压力传感器能测量物体对其正压力的大小,现将质量分别为M、m的物块和小球通过轻绳固定,并跨过两个水平固定的定滑轮(滑轮光滑且较小),当小球在竖直面内左右摆动且高度相等时,物块始终没有离开水平放置的传感器。已知小球摆动偏离竖直方向的最大角度为θ,滑轮O到小球间细线长度为l,重力加速度为g,求:
(1)小球摆到最低点速度大小; (2)小球摆到最低点时,压力传感器示数为0,则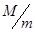 的大小。
的大小。