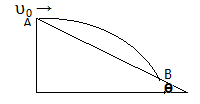
如图1所示,宽度为 的竖直狭长区域内(边界为
的竖直狭长区域内(边界为 ),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为
),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为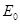 ,
,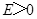 表示电场方向竖直向上。
表示电场方向竖直向上。 时,一带正电、质量为
时,一带正电、质量为 的微粒从左边界上的
的微粒从左边界上的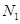 点以水平速度
点以水平速度 射入该区域,沿直线运动到
射入该区域,沿直线运动到 点后,做一次完整的圆周运动,再沿直线运动到右边界上的
点后,做一次完整的圆周运动,再沿直线运动到右边界上的 点。
点。 为线段
为线段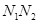 的中点,重力加速度为g。上述
的中点,重力加速度为g。上述 、
、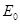 、
、 、
、 、
、 为已知量。
为已知量。
(1)求微粒所带电荷量 和磁感应强度
和磁感应强度 的大小;
的大小;
(2)求电场变化的周期 ;
;
(3)改变宽度 ,使微粒仍能按上述运动过程通过相应宽度的区域,求
,使微粒仍能按上述运动过程通过相应宽度的区域,求 的最小值。
的最小值。
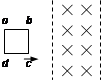
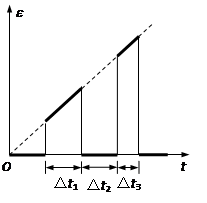

 粤公网安备 44130202000953号
粤公网安备 44130202000953号