截面积为0.2m2的100匝的线圈A,处在均匀磁场中,磁场的方向垂直线圈截面,如图所示,磁感应强度为B =(0.6-0.2t)T(t为时间,以秒为单位),
R1= 3Ω,R2=6Ω,线圈电阻为r = 1Ω,C=3μF,求: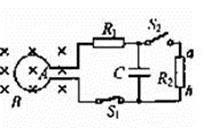
(1)闭合S1、S2后,通过R2的电流大小和方向;
(2)只把S1切断后,通过R2的电量。
相关知识点
截面积为0.2m2的100匝的线圈A,处在均匀磁场中,磁场的方向垂直线圈截面,如图所示,磁感应强度为B =(0.6-0.2t)T(t为时间,以秒为单位),
R1= 3Ω,R2=6Ω,线圈电阻为r = 1Ω,C=3μF,求:
(1)闭合S1、S2后,通过R2的电流大小和方向;
(2)只把S1切断后,通过R2的电量。