如图所示,一根长为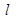 的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
(1)小球带何种电荷,带电量为多少;
(2)如果将细线剪断,小球经时间t发生的位移大小;
(3)若将小球拉至最低点无初速释放,当小球运动到图示位置时受到线的拉力的大小。
如图所示,一根长为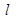 的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
(1)小球带何种电荷,带电量为多少;
(2)如果将细线剪断,小球经时间t发生的位移大小;
(3)若将小球拉至最低点无初速释放,当小球运动到图示位置时受到线的拉力的大小。