杂技中的“顶竿”由两个演员共同表演,站在地面上的演员肩部顶住一根长竹竿,另一演员爬至竹竿顶端完成各种动作后下滑,若竹竿上演员自竿顶由静止开始下滑,滑到竹竿底部时速度正好为零,已知竹竿底部与下面顶竿人肩部之间有一传感器,传感器显示竿上演员自竿顶滑下过程中顶竿人肩部的受力情况如图所示,竹竿上演员质量为m1=40kg,竹竿质量m2=10kg,g=10m/s2.
(1)求竹竿上的人下滑过程中的最大速度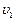 ;
;
(2)请估测竹竿的长度h.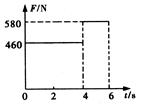
杂技中的“顶竿”由两个演员共同表演,站在地面上的演员肩部顶住一根长竹竿,另一演员爬至竹竿顶端完成各种动作后下滑,若竹竿上演员自竿顶由静止开始下滑,滑到竹竿底部时速度正好为零,已知竹竿底部与下面顶竿人肩部之间有一传感器,传感器显示竿上演员自竿顶滑下过程中顶竿人肩部的受力情况如图所示,竹竿上演员质量为m1=40kg,竹竿质量m2=10kg,g=10m/s2.
(1)求竹竿上的人下滑过程中的最大速度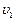 ;
;
(2)请估测竹竿的长度h.