如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点。已知O点是斜坡的起点,斜坡与水平面的夹角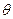 =37°,运动员的质量m=50kg.不计空气阻力。(取sin37°=0.60,cos37°=0.80;g取10m/s2)q求
=37°,运动员的质量m=50kg.不计空气阻力。(取sin37°=0.60,cos37°=0.80;g取10m/s2)q求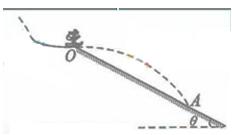
A点与O点时的距离;
运动员离开O点时的速度大小;
运动员落到A点时的动能。
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点。已知O点是斜坡的起点,斜坡与水平面的夹角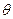 =37°,运动员的质量m=50kg.不计空气阻力。(取sin37°=0.60,cos37°=0.80;g取10m/s2)q求
=37°,运动员的质量m=50kg.不计空气阻力。(取sin37°=0.60,cos37°=0.80;g取10m/s2)q求
A点与O点时的距离;
运动员离开O点时的速度大小;
运动员落到A点时的动能。