如下图a所示,为一组间距d足够大的平行金属板,板间加有随时间变化的电压(如图b所示),设U0和T已知。A板上O处有一静止的带电粒子,其带电量为q,质量为m(不计重力),在t = 0时刻起该带电粒子受板间电场加速向B板运动,途中由于电场反向,粒子又向A板返回(粒子未曾与B板相碰)。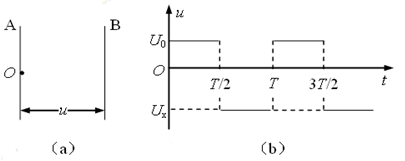
(1)当Ux=2U0时求带电粒子在t=T时刻的动能;
(2)为使带电粒子在t=T时刻恰能能回到O点,Ux等于多少?
相关知识点
如下图a所示,为一组间距d足够大的平行金属板,板间加有随时间变化的电压(如图b所示),设U0和T已知。A板上O处有一静止的带电粒子,其带电量为q,质量为m(不计重力),在t = 0时刻起该带电粒子受板间电场加速向B板运动,途中由于电场反向,粒子又向A板返回(粒子未曾与B板相碰)。
(1)当Ux=2U0时求带电粒子在t=T时刻的动能;
(2)为使带电粒子在t=T时刻恰能能回到O点,Ux等于多少?