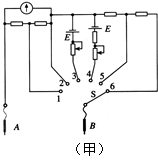
如图所示,A为位于一定高度处的质量为m的小球,B为位于水平地面上的质量为M的长方形空心盒子,盒子足够长,且M = 2m,盒子与地面间的动摩擦因数 =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.
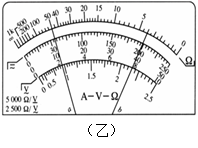


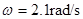 稳定转动后,开始喷漆。仅当狭缝A和B正对平行时,雾滴才能在纸带内侧留下痕迹。改变喷射速度重复实验,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下(如下图)。
稳定转动后,开始喷漆。仅当狭缝A和B正对平行时,雾滴才能在纸带内侧留下痕迹。改变喷射速度重复实验,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下(如下图)。
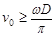 ,则:速度最大的雾滴所留的痕迹应为点,该点离标志线的距离为cm,该喷枪喷出的雾滴的最大速度为m/s,若考虑空气阻力的影响,该测量值真实值(选填“大于”“小于”或“等于”)。
,则:速度最大的雾滴所留的痕迹应为点,该点离标志线的距离为cm,该喷枪喷出的雾滴的最大速度为m/s,若考虑空气阻力的影响,该测量值真实值(选填“大于”“小于”或“等于”)。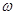 稳定转动。改变喷射速度,重复实验四次。(已知
稳定转动。改变喷射速度,重复实验四次。(已知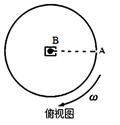
 验装置。
验装置。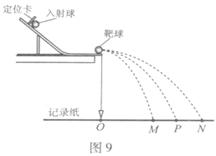
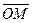 、
、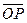 和
和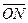 。已知入射球的质量为
。已知入射球的质量为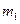 ,靶球的量为
,靶球的量为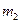 ,如果测得
,如果测得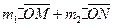 近似等于,则可认为成功验证了碰撞中的动量守恒。
近似等于,则可认为成功验证了碰撞中的动量守恒。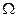 。
。
 ~200
~200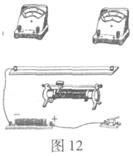


 。通过实验验证了这两次碰撞均遵守动量守恒定律,请你判断
。通过实验验证了这两次碰撞均遵守动量守恒定律,请你判断
 (选填“>”、“<”或“=”)
(选填“>”、“<”或“=”)






 粤公网安备 44130202000953号
粤公网安备 44130202000953号