如图所示，质量m=4kg的物体（可视为质点）用细绳拴住，放在水平传送带的右端，物体和传送带之间的动摩擦因数μ＝0.4，传送带的长度l＝6m，当传送带以v=4m/s的速度做逆时针转动时，绳与水平方向的夹角θ＝37°。已知：g="10" m/s2 ，sin37°="0.6," cos37°=0.8。求：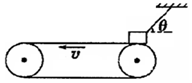
（1）传送带稳定运动时绳子的拉力T；
（2）某时刻剪断绳子，则经过多少时间，物体可以运动到传送带的左端。
如图所示，一定质量的理想气体从状态A经等压过程到状态B.此过程中，气体压强p＝1.0×105 Pa，吸收的热量Q＝7.0×102 J，求此过程中气体内能的增量．
如图所示,位于竖直平面内的光滑轨道,由一段水平的直轨道和与之相切的圆弧轨道ABC连接而成，OC连线与竖直方向夹角为θ=30o。空间中存在一与与水平面成θ=30︒且斜向下的电场，电场强度为E，圆形轨道的半径为R=
m.一质量为m=1kg的小物块带正电，所带电荷量q，且满足Eq=mg。物块在A点获得一初速度，可使得物块恰能在ABC段不离开圆轨道。求：
（1）物块在C点的速度；
（2）物块在A点对轨道的压力；
（3）滑块从C点飞出后到达水平轨道所经历的时间t。
如图所示，水平面上有一个倾角为θ＝30°的斜劈，质量为m。一个光滑小球，质量也为m，用绳子悬挂起来，绳子与斜面的夹角为a＝30°，整个系统处于静止状态。
（1）求出绳子的拉力T；
（2）若地面对斜劈的最大静摩擦力fm等于地面对斜劈的支持力的k倍，为了使整个系统始终保持静止，k值必须满足什么条件？
如图所示，两端开口、粗细均匀的足够长玻璃管插在大水银槽中，管的上部有一定长度的水银，两段空气柱被封闭在左右两侧的竖直管中．开启上部连通左右水银的阀门A，当温度为300 K平衡时水银的位置如图，其中左侧空气柱长度L1=50cm，左侧空气柱底部的水银面与水银槽液面高度差为h2=5cm，左右两侧顶部的水银面的高度差为h1=5cm，大气压为75 cmHg。求：
①右管内气柱的长度L2，
②关闭阀门A，当温度升至405 K时，左侧竖直管内气柱的长度L3．
粤公网安备 44130202000953号