如图是检验某种防护罩承受冲击能力的装置,MN为半径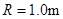 、固定于竖直平面内的
、固定于竖直平面内的 光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径
光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径 的
的 圆弧,圆弧下端切线水平且圆心恰好位于MN轨道的上端点N,M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量
圆弧,圆弧下端切线水平且圆心恰好位于MN轨道的上端点N,M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量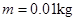 的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求:
的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求: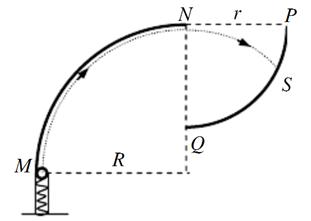
(1)小球到达N点时速度 的大小;
的大小;
(2)发射该钢珠前,弹簧的弹性势能 的大小;
的大小;
(3)钢珠落到圆弧PQ上S点时速度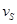 的大小。
的大小。
 =3m/s水平速度从第一块长木板的最左端滑入。已知小物块与长木板间的动摩擦因数
=3m/s水平速度从第一块长木板的最左端滑入。已知小物块与长木板间的动摩擦因数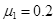 ,长木板与地面间的动摩擦因数
,长木板与地面间的动摩擦因数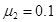 ,设最大静摩擦力与滑动摩擦力相等。重力加速度g取
,设最大静摩擦力与滑动摩擦力相等。重力加速度g取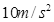 。求:
。求: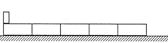
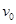 竖直向上抛出,求运动过程中(sin53°=0.8,)
竖直向上抛出,求运动过程中(sin53°=0.8,)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号