(18分) 如图所示,轻质长绳水平地跨过相距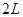 的两个定滑轮A、B上,质量为
的两个定滑轮A、B上,质量为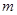 的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力
的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力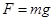 ,先托住物块,使绳处于水平拉直状态. 从静止释放物块,在物块下落过程中,保持C、D两端的拉力
,先托住物块,使绳处于水平拉直状态. 从静止释放物块,在物块下落过程中,保持C、D两端的拉力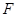 不变,则:
不变,则: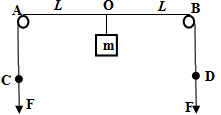
(1)当物块下落距离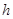 为多大时,物块的加速度为零.
为多大时,物块的加速度为零.
(2)当物块下落上述距离的过程中,克服C端恒力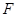 做的功
做的功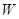 为多少?
为多少?
(3)求物体下落的最大速度 和最大距离
和最大距离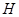 .
.
(18分) 如图所示,轻质长绳水平地跨过相距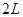 的两个定滑轮A、B上,质量为
的两个定滑轮A、B上,质量为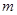 的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力
的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力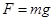 ,先托住物块,使绳处于水平拉直状态. 从静止释放物块,在物块下落过程中,保持C、D两端的拉力
,先托住物块,使绳处于水平拉直状态. 从静止释放物块,在物块下落过程中,保持C、D两端的拉力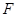 不变,则:
不变,则:
(1)当物块下落距离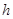 为多大时,物块的加速度为零.
为多大时,物块的加速度为零.
(2)当物块下落上述距离的过程中,克服C端恒力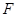 做的功
做的功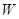 为多少?
为多少?
(3)求物体下落的最大速度 和最大距离
和最大距离 .
.