如图所示为说明示波器工作原理的示意图，已知两平行板间的距离为d、板长为l电子经电压为U1的电场加速后从两平行板间的中央处垂直进入偏转电场，设电子质量为me、电荷量为e。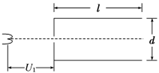
(1)求经电场加速后电子速度v的大小；
(2)要使电子离开偏转电场时的偏转角度最大，两平行板间的电压U2应是多少？
如图，MNP为竖直面内一固定轨道，其圆弧段MN与水平段NP相切于N，P端固定一竖直挡板。M相对于N的高度为h，NP长度为s。一木块自M端从静止开始沿轨道下滑，与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计，物块与NP段轨道间的滑动摩擦因数为μ，求物块停止的地方与N点距离的可能值。
如图所示，物体A放在足够长的木板B上，木板B静止于水平面。t = 0时，电动机通过水平细绳以恒力F拉木板B，使它做初速度为零，加速度aB = 1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mg均为2.0kg，A、B之间的动摩擦因数μ1 = 0.05，B与水平面之间的动摩擦因数μ2 = 0.1，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度g取10m/s2。求
物体A刚运动时的加速度aA
t = 1.0s时，电动机的输出功率P；
若t = 1.0s时，将电动机的输出功率立即调整为P′ = 5W，并在以后的运动过程中始终保持这一功率不变，t = 3.8s时物体A的速度为1.2m/s。则在t = 1.0s到t = 3.8s这段时间内木板B的位移为多少？
如图，一质量m = 1 kg的木块静止的光滑水平地面上。开始时，木块右端与墙相距L = 0.08 m；质量为m = 1 kg的小物块以初速度υ0= 2 m/s滑上木板左端。木板长度可保证物块在运动过程中不与墙接触。物块与木板之间的动摩擦因数为μ= 0.1，木板与墙的碰撞是完全弹性的。取g = 10 m/s2，求
从物块滑上木板到两者达到共同速度时，木板与墙碰撞的次数及所用的时间；
达到共同速度时木板右端与墙之间的距离。
甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变。在第一段时间间隔内，两辆汽车的加速度大小不变，汽车乙的加速度大小是甲的两倍；在接下来的相同时间间隔内，汽车甲的加速度大小增加为原来的两倍，汽车乙的加速度大小减小为原来的一半。求甲乙两车各自在这两段时间间隔内走过的总路程之比。
如图所示，水平放置的平行板电容器，原来两板不带电，上极板接地，它的极板长L = 0.1m，两板间距离d = 0.4cm，有一束相同的带电微粒以相同的初速度先后从两板中央平行极板射入，由于重力作用微粒能落到下板上，微粒所带电荷立即转移到下极板且均匀分布在下极板上。设前一微粒落到下极板上时后一微粒才能开始射入两极板间。已知微粒质量为 m = 2×10-6kg，电量q = 1×10-8 C，电容器电容为C =10-6 F，取g=10m/s2。求：
为使第一个微粒的落点范围能在下板中点到紧靠边缘的B点之内，求微粒入射的初速度
的取值范围；若带电微粒以第一问中初速度
的最小值入射，则最多能有多少个带电微粒落到下极板上。
粤公网安备 44130202000953号