如图所示，玩具射击枪水平放置，玩具枪与目标靶中心位于离地面足够高的同一水平线上，枪口与目标靶中心之间的水平距离s="5" m，子弹射出的水平初速度v为10 m/s，不计空气阻力，重力加速度g为10 m/s2，（靶足够大）求：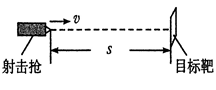
（1）从子弹由枪口射出开始计时，经多长时间子弹击中目标靶；
（2）子弹击中目标靶的位置与靶中心的距离h；
（3）子弹击中目标靶时，子弹的速度大小。
如图甲所示，光滑绝缘水平面上，磁感应强度B=2T的匀强磁场以虚线MN为左边界，MN的左侧有一质量m=0.1kg，bc边长L1=0.2m，电阻R=2Ω的矩形线圈abcd，t=0时，用一恒定拉力F拉线圈，使其由静止开始向右做匀加速运动，经过时间1 s，线圈的bc边到达磁场边界MN，此时立即将拉力F改为变力，又经过1s，线圈恰好完全进入磁场．整个运动过程中，线圈中感应电流i随时间t变化的图象如图乙所示．
（1）求线圈bc边刚进入磁场时的速度v1和线圈在第ls内运动的距离x；
（2）写出第2s内变力F随时间t变化的关系式；
（3）求出线圈ab边的长度L2.
如图所示，在平面坐标系xoy内，第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场，第I、Ⅳ象限内存在半径为L的圆形匀强磁场，磁场圆心在M（L，0）点，磁场方向垂直于坐标平面向外．一带正电粒子从第Ⅲ象限中的Q（一2L，一L）点以速度
沿
轴正方向射出，恰好从坐标原点O进入磁场，
从P（2L，O）点射出磁场．不计粒子重力，求：
（1）电场强度与磁感应强度大小之比
（2）粒子在磁场与电场中运动时间之比
如图所示，将质量m＝0.1kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径。环与杆间动摩擦因数m＝0.8。对环施加一位于竖直平面内斜向上，与杆夹角q＝53°的拉力F，使圆环以a＝4.4m/s2的加速度沿杆运动，求F的大小。（取sin53°＝0.8，cos53°＝0.6，g＝10m/s2）。
如图所示，竖直平面内一光滑水平轨道左边与墙壁对接，右边与一足够高的1／4光滑圆弧轨道相连，木块A、B静置于光滑水平轨道上，A、B质量分别为1.5kg和0.5kg。现让A以6m/s的速度水平向左运动，之后与墙壁碰撞，碰撞时间为0.3s，碰后速度大小变为4m/s。当A与B碰撞后会立即粘在一起运动，已知g=10m/s2 求：
①A与墙壁碰撞过程中，墙壁对小球平均作用力F；
②A、B滑上圆弧轨道的最大高度。
，透明物质II的折射率为n2。一束光线在纸面内沿O点方向射入元件，光线与AB面垂线的夹角到θ时，通过观察发现此时从AC面恰好无光线射出，在BC面有光线垂直射出；
；
粤公网安备 44130202000953号