如图所示,轻杆两端分别系着质量为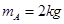 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为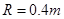 m的1/4圆弧。质量为
m的1/4圆弧。质量为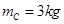 的小球C以
的小球C以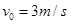 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取 ,则:
,则: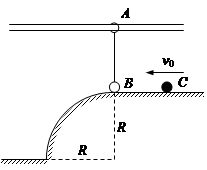
(1)碰后C球平抛的水平位移 (2)碰后瞬间B球的速度 (3)A、B间轻杆的长度
如图所示,轻杆两端分别系着质量为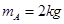 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为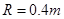 m的1/4圆弧。质量为
m的1/4圆弧。质量为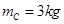 的小球C以
的小球C以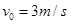 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取 ,则:
,则:
(1)碰后C球平抛的水平位移 (2)碰后瞬间B球的速度 (3)A、B间轻杆的长度