宇航员在一行星上以10m/s的速度竖直上抛一质量为0.2kg的物体,不计阻力,经2.5s后落回手中,已知该星球半径为7220km。
(1)该星球表面的重力加速度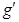 多大?
多大?
(2)要使物体沿水平方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(3)若物体距离星球无穷远处时其引力势能为零,则当物体距离星球球心r时其引力势能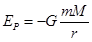 (式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
相关知识点
宇航员在一行星上以10m/s的速度竖直上抛一质量为0.2kg的物体,不计阻力,经2.5s后落回手中,已知该星球半径为7220km。
(1)该星球表面的重力加速度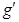 多大?
多大?
(2)要使物体沿水平方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(3)若物体距离星球无穷远处时其引力势能为零,则当物体距离星球球心r时其引力势能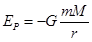 (式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?