在真空中,半径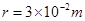 的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度
的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度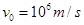 从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷
从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷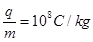 ,不计粒子重力.
,不计粒子重力.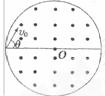
(1)求粒子在磁场中做匀速圆周运动的半径;
(2)若要使粒子飞离磁场时有最大偏转角,求入射时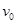 与ab的夹角
与ab的夹角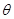 及粒子的最大偏转角.
及粒子的最大偏转角.
在真空中,半径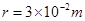 的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度
的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度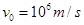 从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷
从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷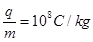 ,不计粒子重力.
,不计粒子重力.
(1)求粒子在磁场中做匀速圆周运动的半径;
(2)若要使粒子飞离磁场时有最大偏转角,求入射时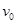 与ab的夹角
与ab的夹角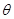 及粒子的最大偏转角.
及粒子的最大偏转角.