直流电动机M和电炉R1并联接到直流电源上,已知电源的电动势为E=100伏,电炉电阻为R1=19欧(恒定不变)。电路如图,当开关S断开时,电炉的功率为475W;当开关S闭合时,电炉的功率是304W,电动机的机械功率为1440W.求①电源内阻r。②电动机绕组的电阻R2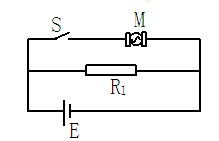
直流电动机M和电炉R1并联接到直流电源上,已知电源的电动势为E=100伏,电炉电阻为R1=19欧(恒定不变)。电路如图,当开关S断开时,电炉的功率为475W;当开关S闭合时,电炉的功率是304W,电动机的机械功率为1440W.求①电源内阻r。②电动机绕组的电阻R2