如图所示，一质量为6kg的物块，置于水平地面上．物块与地面的动摩擦因数为0.5，然后用两根绳分别系在物块的A点和B点，A绳水平，B绳与水平面成37°，已知sin37°=0.6，cos37°=0.8，g取10m/s2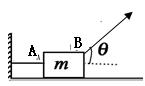
（1）逐渐增大B绳的拉力，直到物块对地面的压力恰好为零，则此时A绳和B绳的拉力分别是多大？
（2）将A绳剪断，为了使物块沿水平面做匀速直线运动，在不改变B绳方向的情况下，B绳的拉力应为多大？
如图所示，xOy坐标系内有匀强磁场，磁感应强度为B，方向垂直纸面向里，x<0区域内有匀强电场(图中未画出)，y轴为电场右边界．磁场中放置一半径为R的圆柱形圆筒，圆心O1的坐标为(2R,0)，圆筒轴线与磁场平行，现有范围足够大的平行电子束以速度v0从很远处垂直于y轴沿x轴正方向做匀速直线运动射入磁场区，已知电子质量为m，电荷量为e，不考虑打到圆筒表面的电子对射入磁场的电子的影响．
求：（1）x<0区域内的匀强电场的场强大小和方向；
（2）若圆筒外表面各处都没有电子打到，则电子初速度应满足什么条件？
（3）若电子初速度满足v0＝
，则y轴上哪些范围射入磁场的电子能打到圆筒上？圆筒表面有电子打到的区域和圆筒表面没有电子打到的区域的面积之比是多少？
如图所示，在一个倾斜的长冰道上方，一群穿相同冰鞋的小孩子排成队，每隔1s有一个小孩从某一起始线开始往下滑，一游客对着冰道上的孩子拍下一张照片，照片上有甲、乙、丙、丁四个孩子，他根据照片与实物的比例推算出乙和甲、乙和丙之间的距离分别为12.5m和17.5m. 若不考虑一切阻力且曝光时间可忽略不计，请你据此求解下列问题：（g取10 m/s2)
(1)冰道的倾角是多少？
（2）拍照时，最下面的小孩丁的速度是多少？
（3）拍照后0.5s时，甲和乙之间的距离是多少？
带电粒子在AB两极板间靠近A板中央附近S处静止释放,在两极板电压中加速,从小孔P平行CD极板方向的速度从CD极板中央垂直进入偏转电场,B板靠近CD板的上边缘如图甲.在CD两板间加如图乙所示的交变电压,设
时刻粒子刚好进入CD极板,
时刻粒子恰好从D板的下边缘飞入匀强磁场,匀强磁场的上边界与CD极板的下边缘在同一水平线上,磁场范围足够大,加速电场AB间的距离,偏转电场CD间的距离及CD极板长均为
,图象乙中
和
都为已知，带电粒子重力不计，不考虑电场和磁场边界影响.求:
（1）加速电压
？
（2）带电粒子进入磁场时的速度？
（3）若带电粒子在
时刻刚好从C极板的下边缘进入偏转电场，并刚能返回到初始位置S处，求
（4）带电粒子全程运动的周期
如图所示，在同一水平面内有相互平行的两条滑轨MN和PQ相距1.0m，垂直于滑轨平面竖直向上的匀强磁场的磁感强度B=1T，垂直于滑轨放置的金属棒ab和cd的质量均为1kg，电阻均为1
（其它电阻不计），与滑轨间的动摩擦因数均
=0.5，先固定cd棒，问:
(1)当向左作用在ab上的拉力F的功率为多少时，才能使ab棒以
=10m／s的速度做匀速直线运动?
(2)若撤去外力，则在ab棒继续运动直到停止的过程中，设通过其横截面的电量为1.9C，则在此过程中ab棒消耗的电能是多少？
(3)若本题中棒cd也不固定，设其它情形和已知数据均不改变，则请判断（1)中拉力的功率是变大还是变小？
，sin37°=0.6，cos37°=0.8。求：
粤公网安备 44130202000953号