如图所示,竖直放置的半径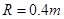 的光滑半圆形细管与水平地面平滑相接,接触处静止一质量
的光滑半圆形细管与水平地面平滑相接,接触处静止一质量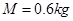 的小球A,另一质量
的小球A,另一质量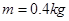 的小球B静止于A右侧。现给小球B一水平向左的瞬时冲量,后经
的小球B静止于A右侧。现给小球B一水平向左的瞬时冲量,后经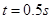 B与 A相碰,碰后瞬间二者结为一体,恰好能沿细管运动至最高点。已知小球B与水平地面间的动摩擦因数
B与 A相碰,碰后瞬间二者结为一体,恰好能沿细管运动至最高点。已知小球B与水平地面间的动摩擦因数 ,重力加速度g取10m/s2。
,重力加速度g取10m/s2。
(1)A、B结合体刚进入圆轨道时对轨道的压力;
(2)小球B在瞬时冲量作用后的速度。
如图所示,竖直放置的半径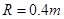 的光滑半圆形细管与水平地面平滑相接,接触处静止一质量
的光滑半圆形细管与水平地面平滑相接,接触处静止一质量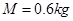 的小球A,另一质量
的小球A,另一质量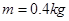 的小球B静止于A右侧。现给小球B一水平向左的瞬时冲量,后经
的小球B静止于A右侧。现给小球B一水平向左的瞬时冲量,后经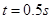 B与 A相碰,碰后瞬间二者结为一体,恰好能沿细管运动至最高点。已知小球B与水平地面间的动摩擦因数
B与 A相碰,碰后瞬间二者结为一体,恰好能沿细管运动至最高点。已知小球B与水平地面间的动摩擦因数 ,重力加速度g取10m/s2。
,重力加速度g取10m/s2。
(1)A、B结合体刚进入圆轨道时对轨道的压力;
(2)小球B在瞬时冲量作用后的速度。