如图所示,AO是具有一定质量的均匀细杆,可绕O轴在竖直平面内自由转动.细杆上的P点与放在水平桌面上的圆柱体接触,圆柱体靠在竖直的挡板上而保持平衡.已知杆的倾角 ,球的重力大小为G,竖直挡板对球的压力大小为
,球的重力大小为G,竖直挡板对球的压力大小为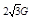 ,各处的摩擦都不计,试回答下列问题:
,各处的摩擦都不计,试回答下列问题:
(1)作出圆柱体的受力分析图;
(2)通过计算求出细杆AO对圆柱体的作用力 和桌面对圆柱体支持力
和桌面对圆柱体支持力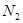 的大小.
的大小.
如图所示,AO是具有一定质量的均匀细杆,可绕O轴在竖直平面内自由转动.细杆上的P点与放在水平桌面上的圆柱体接触,圆柱体靠在竖直的挡板上而保持平衡.已知杆的倾角 ,球的重力大小为G,竖直挡板对球的压力大小为
,球的重力大小为G,竖直挡板对球的压力大小为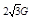 ,各处的摩擦都不计,试回答下列问题:
,各处的摩擦都不计,试回答下列问题:
(1)作出圆柱体的受力分析图;
(2)通过计算求出细杆AO对圆柱体的作用力 和桌面对圆柱体支持力
和桌面对圆柱体支持力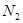 的大小.
的大小.