有一个固定竖直放置的圆形轨道，半径为R，由左右两部分组成。如图所示，右半部分AEB是光滑的，左半部分BFA是粗糙的。现在最低点A给一质量为m的小球一个水平向右的初速度v0，使小球沿轨道恰好能过最高点B，且又能沿BFA回到A点，回到A点时对轨道的压力为4mg。不计空气阻力，重力加速度为g。求：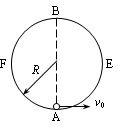
（1）小球的初速度v0大小;
（2）小球沿BFA回到A点时的速度大小;
（3）小球由B经F回到A的过程中克服摩擦力所做的功。
静止的氮核
被速度是v0的中子
击中生成甲、乙两核。已知甲、乙两核的速度方向同碰撞前中子的速度方向一致，甲、乙两核动量之比为1：1，动能之比为1：4，它们沿垂直磁场方向进入匀强磁场做圆周运动，其半径之比为1：6。问：甲、乙各是什么核？写出核反应方程(写出详细的计算过程)。
放在光滑水平面上的物体A和B之间用一个弹簧相连，一颗水平飞行的子弹沿着AB连线击中A，并留在其中，若A、B、子弹质量分别为mA、mB、m，子弹击中A之前的速度为v0，要求求解以后过程中弹簧的最大弹性势能。
某同学给出了如下的解题过程：
三者速度相等时弹性势能最大，由动量守恒得：
还列出了能量守恒方程： 
并据此得出结论。你认为这位同学的解题过程正确吗？
如正确，请求出最大弹性势能的表达式；如果错误，请你书写正确的求解过程并解出最大弹性势能.
已知氢原子基态的电子轨道为r1＝0.528×10－10 m，量子数为n的能级值为
(1)求电子在基态轨道上运动时的动能．
(2)有一群氢原子处于量子数n＝3的激发态．在图上用箭头标明这些氢原子能发出哪几条光谱线．
(3)计算这几条光谱线中波长最短的一条的波长（第三问保留一位有效数字）．
(其中静电力恒量k＝9.0×109 N·m2/C2，电子电量e＝1.6×10－19 C，普朗克恒量h＝6.63×10－34 J·s，真空中光速c＝3.0×108 m/s)
如图所示，AB为固定在竖直平面内的
光滑圆弧轨道，轨道的B点与水平地面相切，其半径为R.质量为m的小球由A点静止释放，求：
（1）小球滑到最低点B时，小球速度v的大小及小球对轨道的压力F压的大小；
（2）小球通过光滑的水平面BC滑上固定曲面，恰达最高点D，D到地面的高度为h（已知h＜R），则小球在曲面上克服摩擦力所做的功Wf.
粤公网安备 44130202000953号