离心轨道是研究机械能守恒和向心力效果的一套较好的器材。如图甲所示，某课外研究小组将一个压力传感器安装在轨道圆周部分的最低点B处，他们把一个钢球从轨道上的不同高处由静止释放。得到多组压力传感器示数F和对应的释放点的高度h的数据后，作出了如图乙所示的F-h图象。不计各处摩擦，取g=10m/s2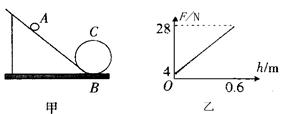 
（1）求该研究小组用的离心轨道圆周部分的半径。
（2）当h="0.6" m，小球到达圆周上最高点C点时，轨道对小球的压力多大?
相关试题
质量为
的物体在水平推力F在作用下沿水平面做直线运动，一段时间后撤去F，其运动的
图像如图所示，
取
，求：
（1）物体与水平面间的动摩擦因数
；
（2）水平推力F的大小；
（3）
内物体运动位移的大小。
物体以
的初速度从斜面底端冲上倾角为
的斜坡，已知物体与斜面间的动摩擦因数为
（
，
，
），求：
（1）物体沿斜面上滑的最大位移；
（2）物体再滑到斜面底端时的速度大小。
一列火车进站前关闭气阀，让车减速滑行，滑行了
时速度减为关闭气阀时的一半，此后又继续滑行了
停在车站。设火车在滑行过程中加速度始终维持不变，试求：
（1）火车滑行的加速度大小。
（2）火车关闭气阀时的速度大小。
（2）从火车关闭气阀到停止滑行时，滑行的总位移。
如图所示，滑雪运动员质量
，沿倾角
的山坡匀加速滑下，经过
的时间速度由
增加到
，
，求：
（1）运动员在这段时间内沿山坡下滑的距离和加速度大小；
（2）运动员受到的阻力（包括摩擦和空气阻力）
，大人用与水平方向成
角斜向上拉力F拉雪橇，使雪橇沿水平地面以
速度做匀速直线运动。已知雪橇与水平地面的动摩擦因数
。（
，
，取
）求：
粤公网安备 44130202000953号