如图所示，在xoy平面的第四象限内存在沿y轴正方向的匀强磁场，场强大小为E，第一象限存在一有界匀强磁场，方向垂直于xoy平面向里，磁感应强度为B，磁场上边界与x轴正向夹角θ=30°，直线MN与y轴平行，N点坐标为（L,0），现从MN上的P点无初速度释放质量为m，电荷量为q的带正电粒子，不计粒子的重力，求：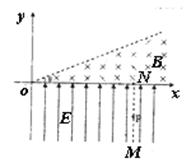
（1）若粒子进入磁场后将垂直于上边界射出磁场，求PN之间的距离；
（2）若粒子进入磁场后能再次回到电场中，则PN之间的距离应满足什么条件？
相关试题
如图所示，质量为m的小物块在粗糙水平桌面上做直线运动，经距离l后以速度υ飞离桌面，最终落在水平地面上．已知l=1.4m，υ="3.0" m/s，m=0.10kg，物块与桌面间的动摩擦因数μ=0.25，桌面高h=0.45m，不计空气阻力，重力加速度g取10m/s2．求：
（1）小物块落地点距飞出点的水平距离s；
（2）小物块的初速度大小υ0．
有一个10匝正方形线框，边长为20 cm，线框总电阻为1 Ω，线框绕OO′轴以10π rad/s 的角速度匀速转动，如图所示，垂直于线框平面向里的匀强磁场的磁感应强度为0.5 T.问：
(1)该线框产生的交变电流电动势最大值、电流最大值分别是多少？
(2)写出感应电动势随时间变化的表达式.
如图所示,位于竖直平面上的
圆弧轨道,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点释放,最后落在水平地面上C点处。不计空气阻力。已知小球到达B点时对圆弧轨道的压力为3mg,求:
(1)小球到达B点时的速度大小。
(2)小球在离开B点前后瞬间的加速度大小。
(3)小球落地点C与B点的水平距离s。
，
，
，求
。
相关知识点
粤公网安备 44130202000953号