(1)在匀强磁场中,有一个原来静止的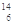 C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
A.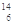 C → C → 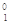 e+ e+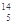 B B |
B.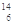 C → C → 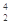 He+ He+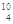 Be Be |
C.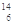 C → C → 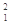 H+ H+ B B |
D.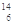 C → C → 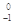 e+ e+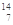 N N |
(2)如图所示,光滑水平面上有带有1/4光滑圆弧轨道的滑块,其质量为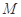 ,一质量为
,一质量为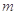 的小球,以速度
的小球,以速度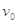 沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
(1)在匀强磁场中,有一个原来静止的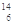 C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
A.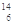 C → C → 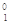 e+ e+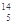 B B |
B.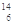 C → C → 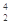 He+ He+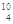 Be Be |
C.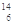 C → C → 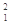 H+ H+ B B |
D.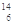 C → C → 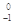 e+ e+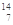 N N |
(2)如图所示,光滑水平面上有带有1/4光滑圆弧轨道的滑块,其质量为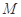 ,一质量为
,一质量为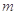 的小球,以速度
的小球,以速度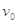 沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?