如图所示,粗细均匀的金属环的电阻为R,可绕轴O转动的金属杆OA的电阻为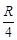 ,杆长为l,A端与环相接触,一电阻为
,杆长为l,A端与环相接触,一电阻为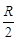 的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。
的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。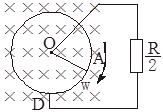
如图所示,粗细均匀的金属环的电阻为R,可绕轴O转动的金属杆OA的电阻为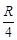 ,杆长为l,A端与环相接触,一电阻为
,杆长为l,A端与环相接触,一电阻为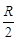 的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。
的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。