如图所示,半径为R的半圆光滑轨道固定在水平地面上。A、B点在同一竖直直线上。质量为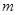 的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为
的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为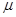 。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。
。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。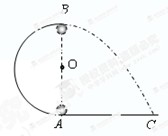
如图所示,半径为R的半圆光滑轨道固定在水平地面上。A、B点在同一竖直直线上。质量为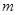 的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为
的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为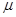 。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。
。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。