如图所示,在半径为R的圆形边界内存在竖直向上的匀强电场,电场强度E=1×106T。以圆心为坐标原点建立直角坐标系,在坐标原点分别以竖直向上、竖直向下,水平向左、水平向右同时抛出四个带正电的小球,小球的电荷量q=8×10-12C,质量m=1×10-6kg,它们的初速度大小均为v0=4m/s,忽略空气阻力,重力加速度g="10m/" s2。则:
(1)当R=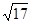 m时,水平向右抛出的小球经过多少时间到达圆形边界?
m时,水平向右抛出的小球经过多少时间到达圆形边界?
(2)试证明,在四个小球都未到达圆形边界前,能用一个圆将四个小球连起来。并写出圆心的坐标。

 ,匀强磁场方向垂直框架平面向上,且B=0.2T,导体捧ab的质量m=0.2kg,R=0.1
,匀强磁场方向垂直框架平面向上,且B=0.2T,导体捧ab的质量m=0.2kg,R=0.1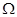 ,水平跨在导轨上,且可无摩擦滑动(g取10m/s2),求;
,水平跨在导轨上,且可无摩擦滑动(g取10m/s2),求;

 粤公网安备 44130202000953号
粤公网安备 44130202000953号