如图所示,斜面的倾角为θ=37o,物块m1和m2之间用轻绳相连,m1=m2=1kg,斜面与m1之间的动摩擦因数为μ=0.25,m2离地面高度h=8m,系统由静止开始运动,假设斜面和轻绳足够长,求:(取g=10m/s2,sin37o=0.6,cos37°=0.8)
(1)m2在落地前瞬间速度多大?
(2)当m2落地后,m1还能向上滑行多远? 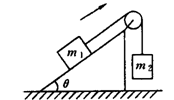
如图所示,斜面的倾角为θ=37o,物块m1和m2之间用轻绳相连,m1=m2=1kg,斜面与m1之间的动摩擦因数为μ=0.25,m2离地面高度h=8m,系统由静止开始运动,假设斜面和轻绳足够长,求:(取g=10m/s2,sin37o=0.6,cos37°=0.8)
(1)m2在落地前瞬间速度多大?
(2)当m2落地后,m1还能向上滑行多远? 