如图所示，在一足够大的空间内存在着水平向右的匀强电场，电场强度大小E＝3.0×104N/C。有一个质量m＝4.0×10－3kg的带电小球，用绝缘轻细线悬挂起来，静止时细线偏离竖直方向的夹角θ＝37°。取g＝10m/s2，sin37°＝0.60，cos37°＝0.80，不计空气阻力的作用。求：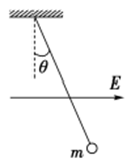
(1)求小球所带的电荷量及电性；
(2)如果将细线轻轻剪断，求细线剪断后，小球运动的加速度大小；
(3)从剪断细线开始经过时间t＝0.20s，求这段时间内小球电势能的变化量。
相关试题
质量为500吨的机车以恒定的功率由静止出发，经5min行驶2. 25km,速度达到最大值54km/h，设阻力恒定。问：
（1)机车的功率P多大？
（2)机车的速度为36 km/h时机车的加速度a多大？
人拉原来静止的重300N的车在水平路面上前进,拉力大小为20N,方向斜向上且与水平方向成300角,车前进500米,车与路面的动摩擦因数为0.03,求:
(1)拉力对车所做的功;
(2)摩擦力对车所做的功;
(3)车获得的动能.
一列简谐横波在x轴线上传播着，在t1=0和t2=0.005s时的波形曲线如图所示：
⑴横波的波长是多大？振幅A是多大？
⑵设周期大于(t2 – t1)，如果波向左传播，波速多大？
⑶设周期小于(t2 – t1)，且波速为6800m/s，求波的传播方向.
如图所示，在真空中有一等腰直角三棱镜ABC，一束单色光以60°的入射角从AB侧面的中点射入，折射后再从AC侧面射出，出射光线偏离入射光线的角度为30°。已知AB =" AC" = d，单色光在真空中的光速为c。
（1）请作出光路图；（2）求单色光通过三棱镜的时间t。
相关知识点
粤公网安备 44130202000953号