如图所示,有一长为L=0.9m的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方,且到O点的距离为h=1.9m,不计空气阻力。(g取10m/s2)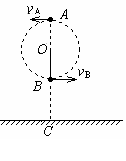
(1)求小球通过最高点A时的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力T恰好为小球重力的6倍,且小球经过B点的瞬间让细线断裂,求小球落地点到C点的距离。
相关知识点
如图所示,有一长为L=0.9m的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方,且到O点的距离为h=1.9m,不计空气阻力。(g取10m/s2)
(1)求小球通过最高点A时的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力T恰好为小球重力的6倍,且小球经过B点的瞬间让细线断裂,求小球落地点到C点的距离。