竖直直杆上有相距L的A、B两点，取一段长为2L的光滑细线，将这段细线穿过一个质量为m的小环（小环半径很小，可忽略不计），然后把细线的一端固定于直杆上的A点，另一端固定于直杆上的B点，再使竖直杆以自身为轴转动，导致小环在水平面内做圆周运动，逐渐缓慢地增加转动的角速度，直到使细线的一部分呈水平状态，如图所示。（重力加速度为g）求：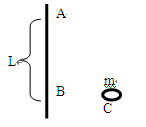
（1）此时，细线上水平部分（即图示BC段）的长度
（2）此时，细线中的拉力大小
（3）此时，系统转动的角速度
相关试题
如图所示，长为L=75cm的平底玻璃管，底部放置一可视为质点的小球，现让玻璃管从静止开始以a1=16m/s2的加速度竖直向下运动，经一段时间后小球运动到管口，此时让玻璃管加速度大小减为a2=2.5m/s2，方向不变，空气阻力不计，取g=10m/s2．求：
（1）小球到达管口时小球和玻璃管的速度；
（2）从玻璃管开始运动到小球再次回到玻璃管底部所用的时间．
如图所示，弹簧AB原长为35cm，A端挂一个重50N的物体，手执B端，将物体置于倾角为30°的斜面上．当物体沿斜面匀速下滑时，弹簧长度为40cm；当物体匀速上滑时，弹簧长度为50cm，试求：
（1）弹簧的劲度系数；
（2）物体与斜面的滑动摩擦系数．
同向运动的甲乙两质点在某时刻恰好通过同一路标，以此时为计时起点，此后甲质点的速度随时间的变化关系为v=4t+12（m/s），乙质点位移随时间的变化关系为x=2t+4t2（m），试求：
（1）两质点何时再次相遇；
（2）两质点相遇之前何时相距最远的距离．
相关知识点
粤公网安备 44130202000953号