如图所示，在倾角为θ的粗糙斜面上，有一个质量为m的物体被水平力F推着静止于斜面上，已知物体与斜面间的动摩擦因数为μ，且μ＜tanθ，设最大静摩擦力等于滑动摩擦力，重力加速度为g，求：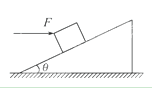
（1）若物体恰好不下滑，则推力F为多少？
（2）若物体恰好不上滑，则推力F为多少？
1935年在苏联的一条直铁轨上，有一列火车因蒸汽不足而停驶，驾驶员把货车厢甲留在现场，只拖着几节车厢向前方不远的车站开进，但他忘了将货车厢刹好，使车厢在斜坡上以4 m/s的速度匀速后退，此时另一列火车乙正以16 m/s的速度向该货车厢驶来，驾驶技术相当好的驾驶员波尔西列夫立即刹车，紧接着加速倒退，结果恰好接住了货车厢甲，从而避免了相撞．设列车乙刹车过程和加速倒退过程均为匀变速直线运动，且加速度大小均为2 m/s2，求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时，两车相距多远？
如图所示，轻弹簧的两端与质量均为2m的B、C两物块固定连接，静止在光滑水平面上，物块C紧靠挡板但不粘连．另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰，碰撞时间极短可忽略不计．（所有过程都在弹簧弹性限度范围内）求：
（1）A、B碰后瞬间各自的速度；
（2）弹簧第一次压缩最短与第一次伸长最长时弹性势能之比．
A、B为竖直墙壁上等高的两点，AO、BO为长度相等的两根轻绳，CO为一根轻杆。转轴C在AB中点D的正下方，AOB在同一水平面上。∠AOB=90º，∠COD=60º。若在O点处用轻绳悬挂一个质量为m的物体，求平衡后绳AO所受拉力的大小。
光滑水平面上放着质量mA=1kg的物块A与质量mB=2kg的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，用手挡住B不动，此时弹簧弹性势能Ep=49J。如图所示，放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R=0.5m，B恰能到达最高点C取g=10m/s2，求
（1）B落地点距P点的距离（墙与P点的距离很远）
（2）绳拉断后瞬间B的速度vB的大小
（3） 绳拉断过程绳对A所做的功W．
粤公网安备 44130202000953号