如图所示，光滑轨道的DP段为水平轨道，PQ段为半径是R的竖直半圆轨道，半圆轨道的下端与水平的轨道的右端相切于P点，一轻质弹簧左端A固定，另一端拴接一个质量为m的小球B，质量也为m的小球C靠在B球的右侧，现用外力作用在C上，使弹簧被压缩了0.4R（弹簧仍在弹性限度内）。这时小球静止于距离P端3R的水平轨道上，若撤去外力，C球运动到轨道的最高点Q后又恰好落回到原出发点。已知重力加速度为g。求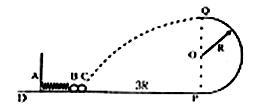
（1）小球C运动到Q点时对轨道的压力多大？
（2）撤去外力前的瞬间，弹簧的弹性势能EP是多少？
如图所示，M为一线圈电阻r=0.4Ω的电动机，R=24Ω，电源电动势E=40V.当S断开时，电流表的示数，I1=1.6A，当开关S闭合时，电流表的示数为I2=4.0A求
（1）电源内阻。
（2）开关S闭合时电动机发热消耗的功率和转化为机械能的功率。
（3）开关S闭合时电源输出功率和电动机的机械效率。
如图所示，阴极K发射电子，阳极P和阴极K间加上电压后电子被加速。A，B是偏向板，使飞进的电子偏离。若已知P，K间所加电压
，A，B两极板长
，A，B两板间距
，所加电压
，
，电子质量
，电子的电荷量
，设从阴极出来的电子速度为零，不计重力。
（1）电子通过阳极P时的速度
是多大？
（2）电子通过偏转电极时具有动能
是多大？
（3）电子过偏转电极后到达距离偏转电极荧光屏上
点，此点偏离入射方向的距离y是多大？
一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘，P为重物，已知P的质量M ="10.5" kg,Q的质量 m ="1.5" kg,弹簧的质量不计,劲度系数 k ="800" N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2 s内,F为变力,0.2 s 以后,F为恒力.求力F的最大值与最小值.(取g ="10" m/s2)
如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(重力加速度g ="10" m/s2)求:
| t ( s ) |
0.0 |
0.2 |
0.4 |
… |
1.2 |
1.4 |
… |
| v( m/s ) |
0.0 |
1.0 |
2.0 |
… |
1.1 |
0.7 |
… |
(1)斜面的倾角α
(2)物体与水平面之间的动摩擦因数μ
(3) t ="0.6" s 时的瞬时速度 v
粤公网安备 44130202000953号