如图8所示, ABCD是由二部分光滑轨道平滑连接在一起组成的,AB为水平轨道,弧BCD的半圆弧轨道,R=2m。质量为M="0.99" kg的小物块,静止在AB轨道上,一颗质量为m=0.01kg子弹水平射入物块但未穿出,物块与子弹一起运动,恰能贴着轨道内侧到达最高点D,并从D点飞出,取重力加速度g=10m/s2,求:
(1)试求子弹刚射入物块时速度的大小;
(2)物块与子弹从D飞出后将落地时的速度大小;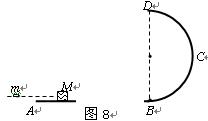
如图8所示, ABCD是由二部分光滑轨道平滑连接在一起组成的,AB为水平轨道,弧BCD的半圆弧轨道,R=2m。质量为M="0.99" kg的小物块,静止在AB轨道上,一颗质量为m=0.01kg子弹水平射入物块但未穿出,物块与子弹一起运动,恰能贴着轨道内侧到达最高点D,并从D点飞出,取重力加速度g=10m/s2,求:
(1)试求子弹刚射入物块时速度的大小;
(2)物块与子弹从D飞出后将落地时的速度大小;