如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN。导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻。有一匀强磁场垂直于导轨平面,磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计。现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行。已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=2m。试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
(1)当金属棒滑行至cd处时回路中的电流多大?
(2)金属棒达到的稳定速度是多大?
(3)当金属棒滑行至cd处时回路中产生的焦耳热是多少?
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,可使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系
式)?
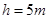 的观景台A,观景台距楼
的观景台A,观景台距楼 .某人在观景台上用球棒将一个硬质小球,向左水平击出,球飞出时的速度口
.某人在观景台上用球棒将一个硬质小球,向左水平击出,球飞出时的速度口
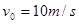 ,空气阻力忽略不计.试求:
,空气阻力忽略不计.试求: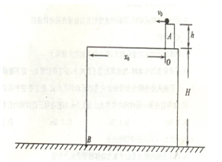
 沿倾角为
沿倾角为 的斜面向上自由滑行,已知雪橇与斜面问动摩擦因数
的斜面向上自由滑行,已知雪橇与斜面问动摩擦因数 ,假设斜面足够长.不计空气阻力。试求:
,假设斜面足够长.不计空气阻力。试求:
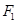 、推力
、推力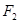 与水平方向的夹角均为
与水平方向的夹角均为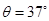 (如图所示),行李箱与地面间为滑动摩擦力,动摩擦因数为
(如图所示),行李箱与地面间为滑动摩擦力,动摩擦因数为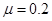 ,行李箱都做匀速运动.试通过定量计算说明是拉箱子省力还是推箱子省力.
,行李箱都做匀速运动.试通过定量计算说明是拉箱子省力还是推箱子省力.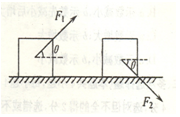
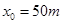 处有一只小狗,如图所示.司机立即采取制动措施.司机从看见小狗到开始制动客车的反应时间为
处有一只小狗,如图所示.司机立即采取制动措施.司机从看见小狗到开始制动客车的反应时间为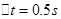 .设客车制动后做匀减速直线运动.试求:
.设客车制动后做匀减速直线运动.试求: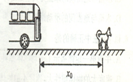
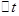 内前进的距离.
内前进的距离.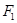 =30N、
=30N、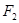 = 40N,请完成下列问题:
= 40N,请完成下列问题: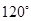 ,规定取1cm长度表示10N,请用作图法作出
,规定取1cm长度表示10N,请用作图法作出 粤公网安备 44130202000953号
粤公网安备 44130202000953号