某物体质量为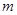 ,在光滑水平面上与运动方向相同的恒力
,在光滑水平面上与运动方向相同的恒力 的作用下,发生一段位移
的作用下,发生一段位移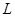 ,速度由
,速度由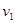 增加到
增加到 。
。
(1)试从牛顿定律出发,导出动能定理的表达式。
(2)运用动能定理解答下面问题,有一质量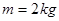 的物体,置于水平面上,在水平恒力
的物体,置于水平面上,在水平恒力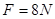 的作用下,使物体由静止开始运动,经过
的作用下,使物体由静止开始运动,经过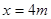 后,撤去
后,撤去 ,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为
,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为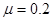 。(
。( 取
取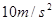 )
)
某物体质量为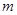 ,在光滑水平面上与运动方向相同的恒力
,在光滑水平面上与运动方向相同的恒力 的作用下,发生一段位移
的作用下,发生一段位移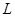 ,速度由
,速度由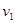 增加到
增加到 。
。
(1)试从牛顿定律出发,导出动能定理的表达式。
(2)运用动能定理解答下面问题,有一质量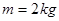 的物体,置于水平面上,在水平恒力
的物体,置于水平面上,在水平恒力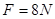 的作用下,使物体由静止开始运动,经过
的作用下,使物体由静止开始运动,经过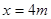 后,撤去
后,撤去 ,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为
,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为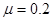 。(
。( 取
取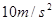 )
)