如图所示，正方形闭合线圈边长为0.2 m，质量为0.1 kg，电阻为0.1 Ω，在倾角为30°的斜面上的砝码质量为0.4 kg，匀强磁场磁感应强度为0.5 T，不计一切摩擦，砝码沿斜面下滑线圈开始进入磁场时，它恰好做匀速运动．(g取10 m/s2)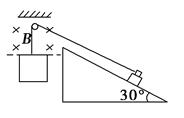
(1)求线圈匀速上升的速度；
(2)在线圈匀速进入磁场的过程中，砝码对线圈做了多少功？
(3)线圈进入磁场的过程中产生多少焦耳热？
如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MN垂直于纸面，在纸面内的长度L＝9.1cm，中点O与S间的距离d＝4.55cm，ON与OS连线的夹角为θ（0<θ<
），板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B＝2.0×10－4T，电子质量m＝9.1×10－31kg，电量e＝－1.6×10－19C，不计电子重力。电子源发射速度v＝1.6×106m/s的一个电子，求：该电子打在板上可能位置的区域的长度l（用含有θ的式子表示）。
在如图所示的竖直平面内，水平轨道CD和长度
的倾斜轨道GH与半径
的光滑圆弧轨道分别相切于D点和G点，GH与水平面的夹角
，过G点、垂直于纸面的竖直平面左侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度
；过D点、垂直于纸面的竖直平面右侧有匀强电场，电场方向水平向右，电场强度
。小物体
质量
、电荷量
，受到水平向右的推力
的作用，沿CD向右做匀速直线运动，到达D点后撤去推力。与轨道CD、GH间的动摩擦因数均为
，取
，
，物体电荷量保持不变，不计空气阻力。求：
（1）小物体到达G点时的速度v的大小；
（2）小物体从G点运动到斜面顶端H点所用的时间
.
如图所示，两平行金属板，板间电场可视为匀强电场，板间距为d，电场强度为E；金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子，由静止开始从正极板出发，经电场加速后射出，并进入磁场做匀速圆周运动。忽略重力的影响，求：
（1）粒子从电场射出时速度v的大小；
（2）粒子在磁场中做匀速圆周运动的半径R。
如图所示，垂直于纸面向里的匀强磁场有明显的圆形边界，圆心为O，半径为R，磁感应强度为B，现在在纸面内放上圆线圈，圆心在O处，半径为r（r<R），共有N匝。求：穿过这个线圈的磁通量。
如图所示，在正交坐标系Oxyz中，分布着电场和磁场（图中未画出）．在Oyz平面的左方空间内存在沿y轴负方向、磁感应强度大小为B的匀强磁场；在Oyz平面右方、Oxz平面上方的空间内分布着沿z轴负方向、磁感应强度大小也为B匀强磁场；在Oyz平面右方、Oxz平面下方分布着沿y轴正方向的匀强电场．在t=0时刻，一质量为m、电荷量为+q的微粒从P点静止释放，已知P点的坐标为（5a，﹣2a，0），电场强度大小为
，不计微粒的重力．求：
（1）微粒第一次到达x轴的速度大小v和时刻t1；
（2）微粒第一次到达y轴的坐标和时刻t2；
（3）假设在平面Oyz存在一层特殊物质，使微粒每次经过Oyz平面时，速度大小总变为原来的
，求在时刻t3=t2+
时，电荷所在位置的坐标．
粤公网安备 44130202000953号