(9 分)如图所示,光滑水平面上的O处有一质量为m=2Kg物体。物体受到两个水平力的作用,F1=4N,F2=(2+2x)N,x为物体相对O的位移。物体从静止开始运动,问: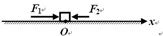
(1)当位移为x=0.5m时物体的加速度多大?
(2)在何位置物体的加速度最大?最大值为多少?
(3)在何位置物体的速度最大?最大值为多少?
(9 分)如图所示,光滑水平面上的O处有一质量为m=2Kg物体。物体受到两个水平力的作用,F1=4N,F2=(2+2x)N,x为物体相对O的位移。物体从静止开始运动,问: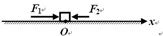
(1)当位移为x=0.5m时物体的加速度多大?
(2)在何位置物体的加速度最大?最大值为多少?
(3)在何位置物体的速度最大?最大值为多少?