在光滑的水平面上,质量为m1的小球A以速率v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1/m2。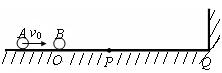
在光滑的水平面上,质量为m1的小球A以速率v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1/m2。