(10分)如图所示,A,B是系在绝缘细线两端、带有等量同种电荷的小球,其中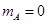 .1 kg,细线总长为20 cm,现将绝缘细线绕过固定于O点的光滑定滑轮,将两球悬挂起来,两球平衡时,OA的线长等于OB的线长,A球依于光滑绝缘竖直墙上,B球悬线OB偏离竖直方向60○,求B球的质量和墙所受A球的压力(g取10 N/kg).
.1 kg,细线总长为20 cm,现将绝缘细线绕过固定于O点的光滑定滑轮,将两球悬挂起来,两球平衡时,OA的线长等于OB的线长,A球依于光滑绝缘竖直墙上,B球悬线OB偏离竖直方向60○,求B球的质量和墙所受A球的压力(g取10 N/kg). 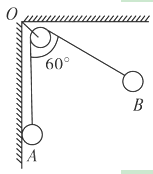
(10分)如图所示,A,B是系在绝缘细线两端、带有等量同种电荷的小球,其中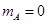 .1 kg,细线总长为20 cm,现将绝缘细线绕过固定于O点的光滑定滑轮,将两球悬挂起来,两球平衡时,OA的线长等于OB的线长,A球依于光滑绝缘竖直墙上,B球悬线OB偏离竖直方向60○,求B球的质量和墙所受A球的压力(g取10 N/kg).
.1 kg,细线总长为20 cm,现将绝缘细线绕过固定于O点的光滑定滑轮,将两球悬挂起来,两球平衡时,OA的线长等于OB的线长,A球依于光滑绝缘竖直墙上,B球悬线OB偏离竖直方向60○,求B球的质量和墙所受A球的压力(g取10 N/kg). 