如图所示，在xOy平面的上、下方，分别有磁感强度为B1、B2的匀强磁场，已知B2=3B1，磁场方向均沿z轴正方向.今有一质量为m、带电荷量为q的带正电荷粒子，自图中O点出发，在xOy平面内，沿与x轴成30°角方向，以初速度v0射入磁场.求：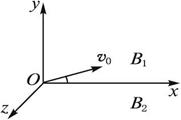
(1)粒子从O点射出到第一次通过x轴的过程中所经历的时间，并确定粒子第一次通过x轴的点的坐标；
(2)粒子从O点射出到第六次通过x轴这段时间内粒子沿x轴方向的平均速度是多少?并画出粒子运动轨迹示意图.
相关试题
某一行星有一质量为m的卫星，以半径r，周期T做匀速圆周运动，求：
（1）行星的质量；
（2）卫星的加速度；
（3）若测得行星的半径恰好是卫星运行半径的1／10,则行星表面的重力加速度是多少？
一物体在光滑水平面上受到水平方向１０Ｎ的恒定拉力的作用，从静止开始经３s速度达到6m/s．求：
(1)这一过程中，拉力所做的功；
(2)第３s末拉力的瞬时功率．
(3)4s内拉力的平均功率。
如图所示，甲为某一波在t=1.0s时的图象，乙为对应该波动的P质点的振动图象。
⑴说出两图中AA’的意义？
⑵求该波速v=?
⑶在甲图中画出再经3.5s时的波形图。
⑷求再经过3.5s时P质点的路程s和位移x。
在波的传播方向上，有相距1.05 m的两质点a、b，当a达正的最大位移时，b恰好在平衡位置.已知a、b间的距离小于一个波长，波的频率为200 Hz，求波传播的速度.
粤公网安备 44130202000953号