(6分)已知氢原子基态电子轨道半径为r0=0.528×10-10 m,量子数为n的激发态的能量En=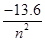 eV.求:
eV.求:
(1)电子在基态轨道上运动的动能;
(2)计算这几条光谱线中波长最短的一条光谱线的波长.(k=9.0×109 N·m2/C2,e=1.60×10-19 C,h=6.63×10-34 J)
(6分)已知氢原子基态电子轨道半径为r0=0.528×10-10 m,量子数为n的激发态的能量En=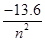 eV.求:
eV.求:
(1)电子在基态轨道上运动的动能;
(2)计算这几条光谱线中波长最短的一条光谱线的波长.(k=9.0×109 N·m2/C2,e=1.60×10-19 C,h=6.63×10-34 J)